使用遗传算法标定VISSIM-4.3（续）

上一篇通过尝试基本款代码，我们发现整体的优化效果并不如意，优化目标值下降值不大，因此我们猜测，原始数据与实际数据可能存在系统误差。

观察原始数据与仿真数据，发现使用我们之前设置的期望速度曲线，跑出来的仿真普遍比实际结果偏慢，这是因为实际的结果是前60*15 min的数据，而仿真使用的期望速度曲线是从 270 * 15 min 组数据筛选出自由流速度数据得到的。（为了加快遗传算法效率我决定数据用60组而不是90组）

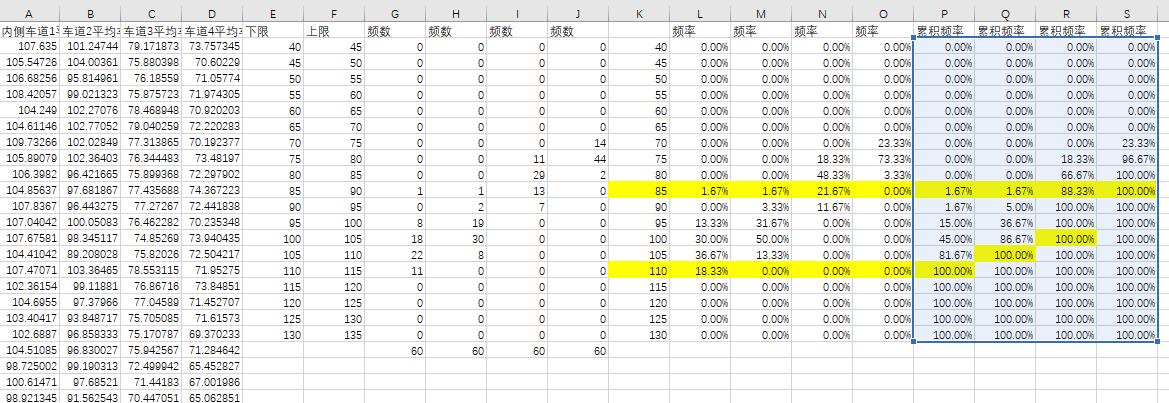
使用60组数据得到的速度累积频率

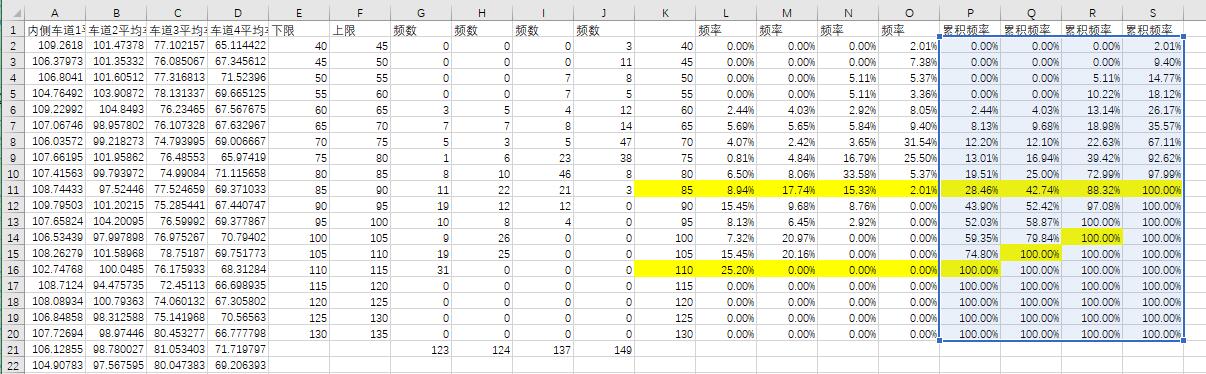
使用自由流数据得到的速度累积频率

可以看到，两组数据形成的累积频率曲线差异还是挺大的，我们在VISSIM中重新绘制期望速度分布曲线，只用速度误差作为目标函数重新进行仿真，控制台打印误差为：

第 0 组参数： CC0= 1.6133525742071577 ,CC1= 2.579484627183955 ,CC2= 3.048217724522928
误差为： 10.736255019064515
第 1 组参数： CC0= 1.630496245956501 ,CC1= 0.939933568656533 ,CC2= 2.119093017543728
误差为： 3.0226755068816686
第 2 组参数： CC0= 1.416860830987368 ,CC1= 2.3135730993770327 ,CC2= 4.0672493706846256
误差为： 8.127507039224755
第 3 组参数： CC0= 1.3607793973691868 ,CC1= 1.8972921210234326 ,CC2= 2.4298498491291585
误差为： 4.043634741465164
第 4 组参数： CC0= 1.6212346529011652 ,CC1= 2.449189064157547 ,CC2= 3.6051459280147946
误差为： 9.11592195513011
第 5 组参数： CC0= 1.4005526732042284 ,CC1= 1.1773221130955975 ,CC2= 6.135465834624824
误差为： 2.988166178479488
第 6 组参数： CC0= 1.5344927280384584 ,CC1= 1.0105229323343183 ,CC2= 6.549979511566051
误差为： 2.983192209746833
第 7 组参数： CC0= 1.5935577666812208 ,CC1= 2.4997559277874197 ,CC2= 3.7182450130484757
误差为： 9.49742740430594
........

从控制台输出可以看出，这一回CC0、CC1、CC2参数的变化对总误差的影响敏感了许多，表明期望速度分布曲线对于标定结果的准确性具有关键性影响 消除由于期望速度分布曲线设置不准确造成的速度误差后，使用遗传算法寻找最优的参数效果才比较好，解释得比较清楚。

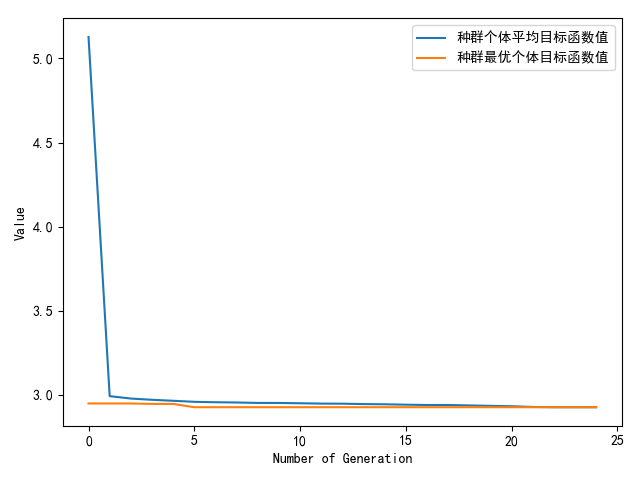
这一回，随着遗传代数增长，目标函数值收敛得比较快，在一个小区域内变化仿真参数对目标函数值影响不是特别大。

最优参数：

CC0	CC1	CC2
1.232534	1.476736	2.466359

最后仿真大约跑了8小时多点，最优代是第6代，最优目标函数值是2.92553318956994，效果拔群。

结论：

期望速度分布曲线对于标定结果准确性影响很大，准确拟合速度曲线有利于消除系统误差。
最后得到的仿真参数的组合可能不是单个最优解，而是形成一片解空间。（不是单个山峰，而是一片高原）