贝叶斯理论:
- 衡量可信度belief(概率是对可信度的度量)
- 有先验概率
- 有后验概率,先验后验都是概率分布
- 先验概率会影响后验概率
- 后验概率由于是一个分布,由此可以得到可信度
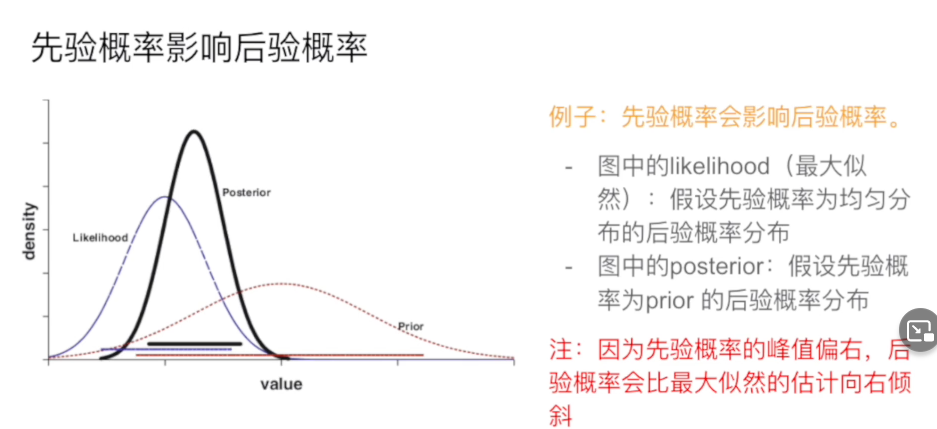
简单来说就是:
- 打麻将算剩下的牌的概率
贝叶斯定理
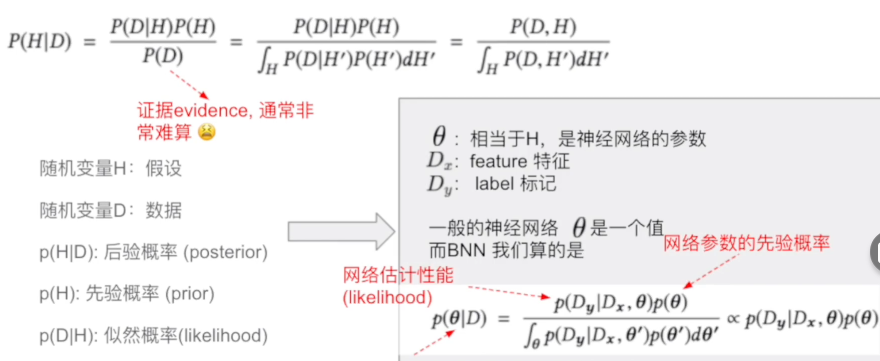
在神经网络里,我们的任务就是要求一个P(H|D),这里D 是data,或者叫evidence,H是假设,通常也就是我们待求的参数。也就是说在观测到D的前提下,算H的概率
普通神经网络可以当做BNN的特例。
怎么设计BNN?
一个神经网络+一个统计模型+先验概率和似然概率
后验概率怎么算?
方法1:MCMC
基本思想:随机采样,然后再采样一个点,如果更好就接受,不然就以一定概率接受。
metropolis-hasting
方法2:变分推断
P(H|D)不好计算,我们用一个参数化的分布(变分分布)去近似得到p(H|D)
他通过一系列推导,把算P(H|D),用一个近似分布拟合P(H|D),目标是让两个分布的KL散度最小(KL散度衡量不同分布之间的距离),通过推导可以得到最小化KL散度等价于最大化ELBO

最大化ELBO经过一系列变量变化可以推导出一个类似反向传播的方法,又叫BBB
模型评价
MAP
Kurtosis
自卑自信
模型缺点
- 模型更加复杂,收敛慢
- 参数太多

