Pytorch学习笔记之搭建两个简单的神经网络（1）

这年头10个研究生，9个搞机器学习，连传统的交通工程学科也不能幸免。作为交通工程师，我发现我在机器学习方面要充电的地方太多了。得赶紧抽空把这一课补上，唉！

一元函数拟合

第一篇尝试用Pytorch搭建两个神经网络，用来拟合不同的函数，作为对Pytorch的熟悉。

首先是最简单的y=x²，来自于B站莫烦的pytorch课程

直接上代码。搭建的神经网络里有两个隐藏层，1个输出层，用线性全连接。隐藏层激活函数使用reLu，优化器使用的Adam，学习率0.1，加上了一些噪声。输入层和输出层都是1维张量，所以in_features和out_features都是1 隐藏层神经元个数取10（其实可以取多个）

import torch
import numpy as np
import torch.nn as nn
import torch.nn.functional as F
import matplotlib.pyplot as plt
class MyNet(nn.Module):
    def __init__(self,in_features,hidden_features,out_features):
        super().__init__()
        self.hidden1=nn.Linear(in_features,hidden_features)
        self.hidden2=nn.Linear(hidden_features,hidden_features)
        self.outLayer=nn.Linear(hidden_features,out_features)
    def forward(self,x):
        x=F.relu(self.hidden1(x))
        x=F.relu(self.hidden2(x))
        out=self.outLayer(x)
        return out
#unsqueeze     扩展维度：返回一个新的张量，对输入的既定位置插入维度 1返回张量与输入张量共享内存，所以改变其中一个的内容会改变另一个。
x=torch.unsqueeze(torch.linspace(-2,2,100),dim=1)
y=x.pow(2)+0.5*torch.rand(x.size())
loss_function=torch.nn.MSELoss()
my_network=MyNet(1,10,1)
optimizer=torch.optim.Adam(my_network.parameters(),lr=0.1)
plt.ion()
plt.show()
for epoch in range(1000):
    predict=my_network(x)
    loss=loss_function(predict,y)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    if epoch%5==0:
        plt.cla()
        print(loss.data)
        plt.scatter(x, y)
        plt.plot(x.data.numpy(),predict.data.numpy(),'r-')
        plt.pause(0.1)
plt.ioff()
plt.show()

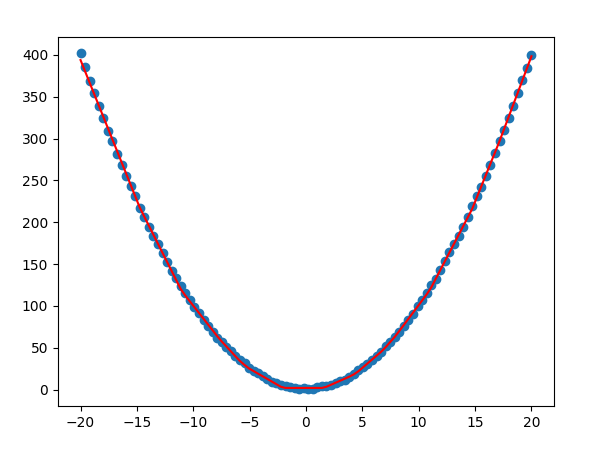
最后输出的结果如图所示。红线是预测的值，蓝点是初始值。看起来学习得有一些过拟合了

2. 二元函数拟合

有了一维的成功实验，还想尝试一下二维的输入，因为现实中预测问题往往是多维自变量输入，为此，尝试拟合圆锥，也就是。
$$
z=sqrt(x^2+y^2)
$$
为了把两个自变量都输入到神经网络，需要把这两个张量合并到一起，注意合并的时候是用的input_features=torch.cat((x,y),dim=1) cat操作里面的dim=1表示两个张量在第一维相加。在本例中，x和y的尺寸是(1000,1)，如果在dim=0相加，则相加完了变成(2000,1)，在dim=1相加，相加完了变成（1000,2）可以看到在dim=几就表示在第几个维度相加。

额外补充：关于张量

高维张量的合并同样也有这个特性，例如https://blog.csdn.net/orangerfun/article/details/104012365提到：

x = torch.rand((2,2,3))
y = torch.rand((2,2,3))
print("dim=0:", torch.cat((x,y),dim=0))
print("dim=1:", torch.cat((x,y), dim=1))
print("dim=2:", torch.cat((x, y), dim=2))
##输出
x: tensor([[[0.2571, 0.9011, 0.7935],
         [0.9308, 0.3267, 0.3290]],

        [[0.6155, 0.4739, 0.7251],
         [0.8025, 0.0424, 0.8101]]])

y: tensor([[[0.8813, 0.1149, 0.7757],
         [0.4733, 0.9003, 0.3300]],

        [[0.2597, 0.5810, 0.2507],
         [0.1220, 0.2260, 0.5620]]])

dim=0: tensor([[[0.2571, 0.9011, 0.7935],
         [0.9308, 0.3267, 0.3290]],

        [[0.6155, 0.4739, 0.7251],
         [0.8025, 0.0424, 0.8101]],

        [[0.8813, 0.1149, 0.7757],
         [0.4733, 0.9003, 0.3300]],

        [[0.2597, 0.5810, 0.2507],
         [0.1220, 0.2260, 0.5620]]])

dim=1: tensor([[[0.2571, 0.9011, 0.7935],
         [0.9308, 0.3267, 0.3290],
         [0.8813, 0.1149, 0.7757],
         [0.4733, 0.9003, 0.3300]],

        [[0.6155, 0.4739, 0.7251],
         [0.8025, 0.0424, 0.8101],
         [0.2597, 0.5810, 0.2507],
         [0.1220, 0.2260, 0.5620]]])
         
dim=2: tensor([[[0.2571, 0.9011, 0.7935, 0.8813, 0.1149, 0.7757],
        		[0.9308, 0.3267, 0.3290, 0.4733, 0.9003, 0.3300]],

        [[0.6155, 0.4739, 0.7251, 0.2597, 0.5810, 0.2507],
         [0.8025, 0.0424, 0.8101, 0.1220, 0.2260, 0.5620]]])

两个形状是（2,2,3）三维张量在第0维cat之后变成了(4,2,3)，在第1维cat之后变成(2,4,3)，在第2维cat之后维度变成(2,2,6)。

另外参考https://blog.csdn.net/pearl8899/article/details/108611965 对张量的维度这个概念有一个更加全面的解释。

2.dim=0的标量

维度为0的Tensor为标量。定义标量的方式很简单，只要在tensor函数中传入一个标量初始化的值即可。标量一般用在Loss这种地方。
3.dim=1的张量

dim=1相当于只有一个维度，但是这个维度上可以有多个分量（就像一维数组一样）.上面例子中的b，可以视作b=[3, 3]，就是一个以为数组。dim=1的Tensor一般用在Bais这种地方，或者神经网络线性层的输入Linear Input，例如MINST数据集的一张图片用shape=[784]的Tensor来表示。
4.dim=2的张量

dim=2的张量一般用在带有batch的Linear Input，例如MNIST数据集的k张图片如果放再一个Tensor里，那么shape=[k,784]。
5.dim=3的张量

dim=3的张量很适合用于RNN和NLP，如20句话，每句话10个单词，每个单词用100个分量的向量表示，得到的Tensor就是shape=[20,10,100]。
6.dim=4的张量

dim=4的张量适合用于CNN表示图像，例如100张MNIST手写数据集的灰度图（通道数为1，如果是RGB图像通道数就是3），每张图高=28像素，宽=28像素，所以这个Tensor的shape=[100,1,28,28]，也就是一个batch的数据维度:[batch_size,channel,height,width]。

————————————————
版权声明：本文为CSDN博主「凝眸伏笔」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/pearl8899/article/details/108611965

pytorch中的tensor维度可以通过第一个数前面的中括号数量来判断，有几个中括号维度就是多少。拿到一个维度很高的向量，将最外层的中括号去掉，数最外层逗号的个数，逗号个数加一就是最高维度的维数，如此循环，直到全部解析完毕。

https://blog.csdn.net/qq_41375609/article/details/106078474

跑题了，回到前述二元函数拟合，这里操作之后，plt绘图对应变成绘制3D。

import torch
import numpy as np
import torch.nn as nn
import torch.nn.functional as F
import matplotlib.pyplot as plt
class MyNet(nn.Module):
    def __init__(self,in_features,hidden_features,out_features):
        super().__init__()
        self.hidden1=nn.Linear(in_features,hidden_features)
        self.hidden2=nn.Linear(hidden_features,hidden_features)
        self.outLayer=nn.Linear(hidden_features,out_features)
    def forward(self,x):
        x=F.relu(self.hidden1(x))
        x=F.relu(self.hidden2(x))
        out=self.outLayer(x)
        return out
x=torch.unsqueeze(torch.rand(1000)*2-1,dim=1)
y=torch.unsqueeze(torch.rand(1000)*2-1,dim=1)
z=torch.sqrt(x.pow(2)+y.pow(2))

input_features=torch.cat((x,y),dim=1) #这个cat的作用是把两个张量合并起来。
loss_function=torch.nn.MSELoss()
my_network=MyNet(2,10,1) #输入张量有2个维度，所以输入特征数是2
optimizer=torch.optim.Adam(my_network.parameters(),lr=0.1)

plt.ion()
plt.show()
ax = plt.axes(projection='3d')  # 设置三维轴
for epoch in range(1000):

    predict=my_network(input_features)
    loss=loss_function(predict,z)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    if epoch%5==0:
        plt.cla()
        print(loss.data)
        ax.scatter3D(x.data.numpy(),y.data.numpy() , z.data.numpy())
        ax.scatter3D(x.data.numpy(),y.data.numpy(),predict.data.numpy(),'r')
        plt.pause(0.1)
plt.ioff()
plt.show()

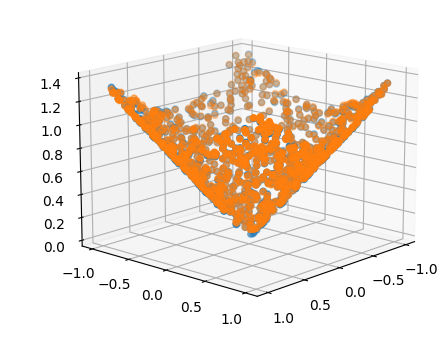
蓝色是原始点，橙色是预测点，感觉还是有一些过拟合2333。

用生成的数据，神经网络拟合的效果还是很好的。可惜现实生活中很难有理想的数据，挑战还是很多的。例如之前听培训的时候听了一个金融风控的例子：在超大的交易数据里通过仅有判别过的数百条异常交易数据，学习异常交易的模式，并用于整个交易数据的风险性判别。看来尽管有能够拟合任意非线性函数工具，但由于数据本身的特性，导致了算法工程师大量的时间还是在调整数据，调整特征。这一点之后学到了用到了再体会吧。